BASIC Stamp II math note #C

BASIC Stamp, CORDIC math implementation-Givens Transform

(updated 5/15/05)

The CORDIC method derives from the Givens transform of linear and matrix algebra.This transform relates the coordinates of a point p in one coordinate system to the coordinates of that same point in another coordinate system that has been rotated by an fixed angle around the origin. This is depicted in figure #A below. The coordinates of the single point p are (x,y) in the black coordinate system, and (x',y') in the red coordinate system. The red coordinates have been rotated by an angle H. (The diagram uses the Greek letter phi instead of H-sorry about that.) The equation relating the coordinates are:

x' = x cos H + y sin H
y' = y cos H - x sin H
   

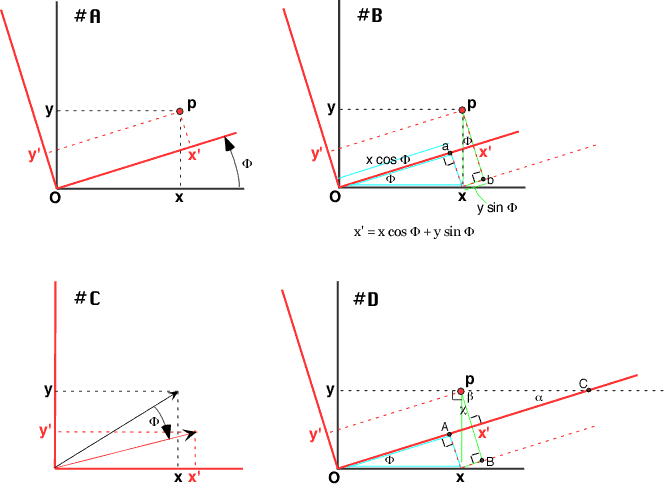
Now, how do you derive that, from geometrical reasoning?  Please refer to  figure B.

1. Construct a line through point (x,0), perpendicular to the x' axis, intersecting at point a.  This line is highlighted in blue in figure B and forms the blue triangle Oax.
2. Construct a line through point (x,0), parallel to line Ox'.
3. Construct a line through point p, pependicular to line Ox' at point x', and also  perpendicular to the line from step 2 at point b.  This line is highlighted in green on figure B and forms the green triangle Pbx.
4. The angle H (phi) subtended by the blue triangle at O is equal to the angle H (phi) subtended by the green triangle at P.   (for reasoning to prove this, see below.)
5. Consider the light blue triangle in figure B. Length Oa is the adjacent side of the right triangle OaX, so the length of Oa equals x cos H. 
6. Consider the  green right triangle, PbX. Segment bX  is the opposite side, so its length equals y sin H. 
7. The segment ax' is equal to the segment xb, so the length of ax' is also y sin H.
8. The sum of the two lengths Oa and ax' is x cos H + y sin H, which is the first equation above.
   x' = x cos H + y sin H
9. The second equation follows from similar reasoning, applied to the y axis.
   y' = y cos H + x sin H
10. The same reasoning also works in the second third and fourth quadrant, that is, to any degree of angular rotation, to the full circle.

Figure #D justifies the claim that the top angle in the green triangle (chi in figure D) is equal to the original angle, phi (same as H). The horizontal line through points y and c is constructed parallel to the x axis. Angle alpha is equal to angle phi, because Oc cuts two parallel lines and phi and alpha are on opposite sides. Triangle pcx' is a right triangle, so the sum of angles alpha and beta must equal 90 degrees. Likewise, line px is constructed perpendicular to the x axis and to line yc. So the sum of chi plus beta must also equal 90 degrees. That means that chi equals alpha equals phi, which was to be proved.

Figure #C illustrates how the rotation of coordinates is related to rotation of a vector. The original vector from O to the point (x,y) is rotated through an angle -H to a new position with its tip at (x',y'). Now we have moved the point instead of the coordinate system. The transform of the coordinates is the same as above, except that now we have the angle -H instead of +H. So the sign changes as follows:

vector rotation;
note sign of the sin H terms are reversed, compared with coordinate transform above
    
x' = x cos H - y sin H
y' = y cos H + x sin H

<top> <index> <home> < mailto:info@emesystems.com >