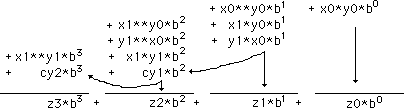Stamp II math note #6
BASIC Stamp, double precision math
(c) 1998, 2001EME Systems, Berkeley CA
U.S.A.
Tracy Allen
(<stamp
index> <home>
contents (updated 1/15/2007)
Sometimes it is necessary to do double precision math, using more
than 16 bits. An example might be computation of an average and
standard deviation. The accumulations mount up rapidly, especially
the sum of the squares.
Multiple precision addition, subtraction and multiplication are
easy to implement, while division is much more problematic and will
require the largest section in this essay.
|
Simple counter, counts up
to 655250000
|
top
|
Sometmes all you need is a simple event counter that can go higher
than 65535. It takes two words, double precision. The least
significant word in the following routine counts up to 9999 and then
rolls over back to zero instead of continuing on to 10000. The high
word then counts up to 65535. If you need a higher count, you could
also roll over the second word at 10000, and have the third word
count up to 65535, for a total of 6553500000000. It would take a
while for the stamp to count that high!
x0 var word ' low word of the count
x1 var word ' high word
x0=9990 ' arbitrary starting value
loop:
x0=x0+1//10000 ' up to 9999
x1=x1 + 1-(x0 max 1) ' ten-thousands
' note the term in () equals zero only when x0=0
' so x1 is incremented only when x0 rolls over from 9999 to 0000
debug dec x1,dec4 x0,cr ' display double precision
next
|
Double precision addition,
negation, subtraction
|
top
|
There are several ways of representing double precison numbers.
The two words can represent a 32 bit positive number in a 16:16
format, or they can represent a 31 bit + sign number in twos
complement format, with the high bit of the high word being the sign.
Another convenient notation for addition
and subtraction and division is 15:15, where the high bit of each
word is reserved as a carry, and the high bit of the most significant
word is reserved as a sign if necessary. However, this is not so
convenient for multiplication.
The following subroutines are presented without much comment,
except for the number format expected. So much of math on the stamp
is ad hoc, there to solve a specific problem. The Stamp does not have
enough horsepower support any fancy general purpose computation
engine. The math routines for a project should do the minimum to get
the job done reliably and economically in terms of code space and
execution time. Additional analysis will be necessary in each case to
determine the limits of the variables and where the formulas might
fail as they run up against and beyond those limits. For example, the
multiply routine will give misleading results if the actual product
might be greater than 2^32.
' various ad hoc double precision math subroutines
' Tracy Allen, http://www.emesystems.com
z1 var word
z0 var word
y1 var word
y0 var word
x1 var word
x0 var word
cb var bit ' carry out of double prec add
' borrow from double prec subtract
Addtion with both double precision variables represented as 16 bit
values. This uses the max operator to detect the carry from the low
word to the high word.
add1616: ' Z=X+Y in 16:16 notation
z0=x0+y0
z1=x1 + y1 + (z0 max x0 - x0 max 1)
return
The term in parentheses above is the carry from the first addition.
There is a carry only if z0 is less than x0 ( and if so it will also be
less than y0.) Remember that x0, y0 and z0 are 16 bit
unsigned numbers. If there is a sign, for twos complement,
it will calculate correctly as bit 15 of the high words.
Here is a less tricky way to handle the carry,
and to compute a carry to another word. Note that the carry to another
word
is taken in two stages, because the carry can arise from either of the
two additions.
add1616: ' Z=X+Y in 16:16 notation
cb=0
z0=x0+y0
z1=x1+y1
IF z1< x1 THEN cb=1
IF z0<x0 THEN ' the comparison could just as well be y0
z1=z1+1 ' carry from addition x0+y0
IF z1=0 THEN cb=1 ' carry from addition z1+1
ENDIF
return
Then there is addtion with both double precision variables
represented as 15 bit
values. The 16th bit serves as the carrry. This is most useful as
part of a longer routine, where the variables will be in 15:15
notation anyway.
add1515: ' Z=X+Y in 15:15 notation
z0=x0+y0
z1=x1+y1+z0.bit15 ' adjust back to 15:15
z0.bit15=0
cb=z1.bit15 ' carry out of double precision add
z1.bit15=0
return
Negation of a variable in twos complement notation. Both words are
16 bits, but the 16th bit of the high word is the sign. Zero for
positive, 1 for negative.
negate: ' X=-X in 16:16 notation
x0 = ~x0+1 ' ~ is the NOT operator -- this is the squiggle symbol, not minus!
x1 = ~x1+1-(x0 max 1)
return
The above formula comes directly from the operation of twos
complement arithmetic.
Complement the number (the ~ operator in PBASIC), and then add one. A
carry can occurs
only in the addition of 1, and only when the resulting x0 is zero..
Here is another way to do it:
negate: ' X=-X in s15:16 notation
x0 = ~x0 + 1 ' ~ is the NOT operator
x1 = ~ x1 ' also NOT x1
IF x0=0 THEN x1=x1+1 ' add carry only if final x0 is zero.
return
Now, here is how to do subtraction with both double precision
variables represented as 16
bit values. The 16th bit of the high word can be the sign, as
above.
sub1616: ' Z=X-Y in s15:16 notation
z0=x0-y0
z1= x1 - y1 - (z0 MIN x0 - x0 MAX 1) ' or use (x0 MAX y0 - y0 MAX 1)
return
The
term in parentheses above is the borrow, which occurs if z0 is
greater than x0, or equivalently, if x0 is less than y0, or
equivalently, if z0 is less than y0. Here is an
alternative form using IF instead of calculation for the carry:
sub1616: ' Z=X-Y in s15:16 notation
z0=x0-y0
z1= x1 - y1
IF z0 > x0 THEN z1=z1-1
return
Here is another way to handle the borrow,
and to compute a borrow from the overal calculation. Note that the
borrow to another word
is taken in two stages, because it can arise from either of the two
subtractions.
sub1616: ' Z=X-Y in 16:16 notation
cb=0 ' this is the overall borrow
z0=x0-y0
z1=x1-y1
IF z1 > x1 THEN cb=1 ' borrow from x1-y1, could use (IF x1<y1 THEN cb=1)
IF z0 > x0 THEN ' or could use (IF x0<y0 THEN cb=1)
z1=z1-1 ' borrow from x0-y0
IF z1=-1 THEN cb=1 ' borrow if z1 rolls over to -1
ENDIF
return
I show alternative forms, because sometimes you need to minimize the
number of variables. You can reuse a variable on the left that also
appears on the right.
Subtraction with both double precision variables represented as 15
bit values, but the 16th bit of the high word is the sign. The 16th
bit of the low word serves as the borrow bit. This is most useful as
part of a longer routine, where the variables will be in 16:15
notation anyway.
sub1515: ' Z=X=Y in 15:15 notation
z0=x0-y0
z1=x1-y1-z0.bit15
z0.bit15=0
cb=z1.bit15 ' borrow from double prec. subtract
z1.bit15=0
return
Test for zero is simple. To be zero, all bits in both words have to
be zero:
zeroTest1516: '
zeroFlag = x0 | x1 MAX 1
return
To test for negative, simply test the high bit. That
applies of course only if the numbers are represented in twos
complement form.
minusTest1616: '
minusFlag = x1.bit15
return
Test for greater than or less than requires a subtraction:
magnitudeTest1516: ' Z,X,Y in 15:16 notation
GOSUB sub1616 ' finds z1:z0 = x1:x0 - y1:y0
compareBit = z1.bit15 ' 0 iff x1:x0 >= y1:y0
' z1:z0 is the difference in twos complement format
return
Absolute value is conditional negation
abs1516: ' x1:x0 in 15:16 notation
IF x1.bit15 THEN
x0 = ~x0+1 ' note the ~ squiggle in front. That is bitwise NOT, complement all bits.
x1 = ~x1+1-(x0 max 1)
ENDIF
return
That follows from the definition of twos complement, the complement of
all bits, plus 1.
|
Double and quad
precision multiplication
|
top
|
The Stamp uses the ** operator to return the high word of a double
precision multiply. When two 16 bit numbers, x0 and y0 are multiplied
together, the result is double precision, contained in two words z1
(the high word) and z0 (the low word) written like this with a colon,
z1:z0. Here is a demo program:
' demo program, multiplication of x * y = z
' x and y entered at prompts can each be up to 16 bits
' and product z may be up to 32 bits, double precision.
x0 var word
y0 var word
z1 var word
z0 var word
loop:
debug cr,"xxxx:"
serin 16,$54,[hex4 x0] ' you enter the first number (HEX)
debug cr,"yyyy:"
serin 16,$54,[hex4 y0] ' you enter the second number (HEX)
z0= x0 * y0 ' low word of product
z1= x0 ** y0 ' high word of product
debug cr,hex4 x0," * ",hex4 y0," = "
debug hex4 z1,hex4 z0,cr ' display double precision result (HEX)
goto loop
You can bring out your hex calculator to check the results. In a
later section, I show how to convert the double precision HEX number
to decimal.
Quad precision
What if you need to deal with even larger numbers? Suppose you
have to multiply together two numbers that are already double
precision (32 bits each, two 16 bit words). That yields a result of
up to 64 bits (four 16 bit words). Two double precision numbers x1:x0
and y1:y0 multiplied together give a quadruple precision result,
z3:z2:z1:z0. Here is a general purpose routine:
' {$STAMP BS2}
x0 var word ' x1:x0 for double precision input
x1 var word
y0 var word ' y1:y0 for double precision input
y1 var word
z0 var word ' z3:z2:z1:z0 for quad precision product
z1 var word
Z2 var word
z3 var word
cy var nib ' carry accumulator
loop:
debug cr,"xxxxxxxx:" ' you enter the first number (HEX)
serin 16,$54,[hex4 x1,hex4 x0] ' eg a156fd5c
debug cr,"yyyyyyyy:" ' you enter the second number (HEX)
serin 16,$54,[hex4 y1,hex4 y0]
gosub make4product
debug cr,hex4 x1,hex4 x0," * ",hex4 y1,hex4 y0," = "
debug hex4 z3,hex4 z2,hex4 z1,hex4 z0,cr ' display quad precision result
goto loop
make4product ' subroutine
z0= x0 * y0 ' low word of product
'z1= (x0**y0) + (x0*y1) + (x1*y0) ' possible shortcut, see note 1
z2= x0 ** y0 ' second word of product
z1= x1 * y0 + z2 ' includes cross terms
cy= z1 max z2 - z2 max 1 ' and carry from addition
z2= y1 * x0 ' other cross term
z1= z1 + z2
cy= z1 max z2 - z2 max 1 + cy ' and carry from last addition
'z2= cy +(x1*y1) + (y1**x0) + (x1**y0) ' possible shortcut, see note 2
z2= x1 * y1 + cy ' third word of product, note carry from z1 term
cy= z2 max cy - cy max 1 ' start new carry from additon
z3= x1 ** y0 ' cross term
z2= z2 + z3 ' add
cy= z2 max z3 - z3 max 1 + cy ' carry
z3= y1 ** x0 ' other cross term
z2= z2 + z3 ' add
cy= z2 max z3 - z3 max 1 + cy ' carry
z3= y1 ** x1 + cy ' last term, note carry from z2 term
return
You can check the results with your HEX calculator (if it goes
that high). Try
11111111 x 11111111 = 0123456787654321
or
ffffffff x ffffffff = fffffffe00000000
possible shortcuts...
note 1: if it is known in advance that the result will not
exceed 32 bits, so that it can be held in two words, then the formula
can be cut off at the first shortcut. For example, the first word
might be limited to less than 2^17, and the second word limited to
less than 2^14, then the result will be less than 2^31 and will fit
in two words. Sometimes you just know that when one argument is large
the other will be small.
note 2: if it is known in advance that the result will not
exceed 48 bits, so that it can be held in three words, then the
formula can be cut off at the second shortcut.
If either of those shortcuts apply, then delete all the code
following the shortcut, up to the return instruction, and take the '
off of the shortcut instruction, so that it will be executed as the
last instruction in the make4product subroutine. The extra steps are
really calculating the same values as in the shortcuts. The extra
steps are necessary to keep track of the carry. The shortcut is
possible because it is known in advance that there will be no
carry.
|
Theory. Each multiple precision quantity is represented
as a polynomial in base b=2^16=65536.
X = x1*b + x0
Y = y1*b + y0
Z = X*Y
= (x1*b + x0) * (y1*b + y0)
= (x1*y1)*b2+ (x1*y0 + y1*x0)*b1 + (x0*y0)*b0
for example, the number, X=66091 will be be represented in the
stamp as two words, x1=1, x0=555. That is because 66091 = 1* 65536+555.
Another example, the number Y=328680, will be represented in the Stamp
as two words, x1=5, x0=1000. That because = 5* 65536 + 1000
Each product between two words, such as x0*y0, can result both
a in b0 and a b1 term. The b1 term is
written x0**y0. For example, 555*1000 = 555000, which in the stamp
takes up two words, 555000=8*65536+30712, with x0**y0=8 and x0*y0=30712.
Breaking it down by term for the stamp math, the powers of the
base add up in the columns as follows. Note that there can be a carries
from the addition. There are (cy1) from b1 column to the b2 column, and
a carry (cy2) from the b2 column to the b3 column.
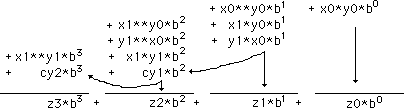
|
Example: multiplication of a 24 bit variable times a 24+ bit
improper fraction.
Suppose that you need to multiply a 24 bit variable obtained from
some instument, times a fixed constant, say, 3.7305512. The fixed
constant is a fraction, and has about 8 decimal digits, about 24
bits, of precision. This might be a result obtained from one of the
new 24 bit analog to digital converters. What do you do if your
calculation has to maintain 24 bits of precision? The */ operator and
the ** operators can maintain 8 bits and 16 bits of precisions
respectively. But that is not good enough here. But the idea is good.
The ** operator approximates any fraction by using a denominator of
65536. Greater precision can be achieved by using 16777216 (which
happens to be 224) as the denominator of the approximating
fraction.
The first step is to get out your scientific calculator, and
multiply the fixed constant times 2 to the 24th power:
3.7305512 * 16777216 = 62671492 rounded off to integer
The way to look at this is
3.7305512 = 62671492 / 16777216
That is the same as saying the fraction with the denominator of
16777216 is almost the same and the fraction with the denomiator of
10000000.
37305512/10000000 ~= 62671492/16777216
Now figure out what it takes to represent the number 62671492 in
binary, using 2 words, 32 bits maximum. The number uses 26 bits, 24
for the fractional part, and 2 for the integer part.
y1 = int (62671492/65536) = 956 to get the high word
y0 = 62671492 - c1*65536 = 19076 to get the low word
Observe that 956/256=3, the integer part of the desired
multiplier. Then here is the PBASIC program to calculate the result
when the variable is multiplied by that constant. This will use the
same make4product subroutine as above.
' {$STAMP BS2}
x0 var word ' x1:x0 for double precision variable
x1 var word
y0 con 19076 ' y1:y0 for double precision constant
y1 con 956
z0 var word ' z3:z2:z1:z0 for quad precision product
z1 var word
Z2 var word
z3 var word
cy var nib ' carry accumulator
loop:
debug cr,"xxxxxxxx:" ' you enter the first number (HEX)
serin 16,$54,[hex4 x1,hex4 x0] ' eg a156fd5c
gosub make4product ' same subroutine as above
z0.byt0=z1.byte1 ' shift right 24 bits, 3 bytes
z0.byte1=z2.byte0 ' division by 2^24
z1.byte0=z2.byte1 ' = 16777216
z1.byte1=z3.byte0
debug cr,hex4 x1,hex4 x0," ****/// ",hex4 y1,hex4 y0," = "
debug hex4 z1,hex4 z0,cr ' display quad precision result
goto loop
After the multiplication, the final result is found by shifting 24
bits to the right, implemented as a move of all the bytes three byte
positions to the right. The program assumes that the result will in
fact fit into 32 bits, that z3.byte1 will be zero, not a bad
assumption starting with 24 bit times 26 bit multiplication, followed
by a 24 bit shift right, which should give a 26 bit or fewer result.
This implementation is like the */ and ** operations in the BASIC
Stamp, and I have stuck in the "***///" symbol to designate this
multiplication/division combination. The variable and the result are
displayed from the debug commands as hex values, so you can check the
results on a good calculator. (see below for an algorithm to convert
the double precision values to decimal, if necessary.)
|
Double precision
division, division by a constant
|
top
|
- Method 0 works when the divisor is a
power of two. It is simply shifting a certain number of places to the
right. Say there is a an average, and it can be arranged to have
exactly 64 samples, then this method can be used to compute the average
at the end. This method is easy to extend to multiple bytes arithmetic.
The previous example (multiplication of a 24 bit variable times a 24+
bit improper fraction) used this form of division in the final step, to
calculate a high precision fractional value of a number.
- Method 1 works when the divisor is a
constant like 10 or 100. Ten is a useful divisor when you want to kick
out decimal digits of a double precision number--you have to do it this
way because the built-in DEC modifiers and the DIG operator do not work
on double precision numbers. Hundred is a useful modifier for
calculation of percents.
Method 0: shifting, divisor a power of
two.
Division by powers of two is easy. It reduces to shifting all 32
bits a certain number of places to the right. Here is an example, of
a divide by 64, with two words representing 16:16 bit composite
value:
' double precision number divided by 256
X var word ' for random numbers
N1 var word ' high word of number
N0 var word ' low word of number
Dv con 6 ' divisor, as power of 2: divisor=2Dv e.g. 26=64
X1 var word ' high word of quotient
X0 var word ' low word of quotient
Xr var byte ' remainder from the division
loop:
random X ' pick a 32 bit number
N1=X
random X
N0=X
debug cr,hex4 N1,hex4 N0," / ",hex4 dcd dv ' show dividend and divisor as hex
Xr = dcd Dv-1&N0 ' find remainder by anding with a mask
' e.g., when Dv=6, then (dcd 6 - 1)=63=%00111111
' these dv bits will be shifted
' out and "fall off" the right end.
X0=N1<<(16-Dv)|(N0>>Dv)
' ^^^^^^--------shift lower word Dv bits right,
'^^^^^^---------and fill on the left with Dv bits from the upper word
X1=N1>>Dv ' divide upper word by Dv
debug " = ",hex4 X1,hex4 X0," remainder= ", hex Xr ' show result
pause 1000
goto loop
Method 1: divisor is a
constant<65536.
We start with a double precision number, represented in two words
z1:z0. Suppose we need to divide the number by 10 or by 100? The
result will in general be a double precision number q1:q0, along with
a remainder, r0. Let's start with specific useful examples. All of
the following use the following variables:
z1 var word ' two words z1:z0 double precision
z0 var word
q1 var word ' output, quotient, z/divisor
q0 var word
rm var word ' remainder from the division, z//divisor
Division by 100...
' calculate z/100, were z=z1:z0, two words
q1=z1/100
q0=z1//100
rm=q0*36//100+(z0//100)
q0=(q0*655)+(q0*36/100)+(z0/100)+(rm/100)
rm=rm//100
Division by 10...
' calculate z/10, were z=z1:z0, two words
q1=z1/10
q0=z1//10
rm=q0*6//10+(z0//10)
q0=(q0*6553)+(q0*6/10)+(z0/10)+(rm/10)
rm=rm//10
To extract the decimal digits of a double precision number,
execute the above routine repeatedly, until there is nothing left.
The remainders at each step are the decimal digits, witht the least
significant first out. Another way to do it is by dividing by 100,
1000 or 10000 at each step. That will extract 2, 3 or 4 digits at
once that can be stored and then printed out using the DEC
modifier.
Division by 1000...
' calculate z/1000, were z=z1:z0, two words
q1=z1/1000
q0=z1//1000
rm=((q0**536*536//1000)+(q0*536)//1000+(z0//1000)) ' <-- corrected parens, //1000 divides entire term in q0536*
q0=(q0*65)+(q0**35127)+(z0/1000)+(rm/1000)
rm=rm//1000
Note the extra "double precision" term in the calculation of the
remainder for division by 1000 . This is because q0*536 can be as
high as 999*536, which is greater than 65536 and leads to an extra
double precision term. See the theory section.
Division by 60, for time calculations...
' calculate z/60, were z=z1:z0, two words
q1=z1/60
q0=z1//60
rm=q0*16//60+(z0//60)
q0=(q0*1092)+(q0*16/60)+(z0/60)+(rm/60)
rm=rm//60
Given two numbers x and y, word variables, compute (x*y)/100,
where x*y may require a double precision number.
' calculate x*y/100, were x*y>65536
q1=x**y/100
q0=x**y//100
rm=q0*36//100+(z0//100)
q0=(q0*655)+(q0*36/100)+(z0/100)+(rm/100)
The general formula, where the divisor is dv, a constant known in
advance at compile time. In the examples, dv was 100, 10, 60 and
1000. Here is the formula when dv<257:
' calculate z/dv, were z=z1:z0, two words
' in addition to the above variables
dv var byte ' dv<256
' precompute the following factors on a calculator
A con ..... ' A=65536/dv, integer division
B con ..... ' B=65536//dv, the remainder from division A
q1=z1/dv
q0=z1//dv
rm=q0*B//dv+(z0//dv)
q0=(q0*A)+(q0*B/dv)+(z0/dv)+(rm/dv)
rm=rm//dv
Note that the BASIC Stamp cannot calculate the constants A and B
directly, because of the number 65536 exceeds one word in size.
Please see a section below on how to get around this limitation and
have dv be a run-time variable.
If the divisor dv is greater than 255 then use the following.
Please test it carefully and look at the theory in the box. I have
not analyzed it for all divisors; in fact, it fails for most large
divisors.
' calculate z/dv, were z=z1:z0, two words
' in addition to the above variables
dv var word ' dv<65536
' precompute the following factors on a calculator
A con ..... ' A=65536/dv
B con ..... ' B=65536//dv, the remainder from division A
C con ..... ' C= B/dv*65536
q1=z1/dv
q0=z1//dv
rm=((q0**B*B//dv)+(q0*B)//dv+(z0//dv))
q0=(q0*A)+(q0**C)+(z0/dv)+(rm/dv)
rm=rm//dv
Another observation:
Let a double precision number be contained in two words,
N=n1:n0
find the remainder N//D, where the divisor is one word, and
satisfies 0<D<65536. Note that this remainder too will be a
single precision word.
Y = {N//D} = (65536//D) * (n1//D) + (n0//D)
When D is a constant, the factor 65536//D can be precomputed. The
restriction is that 65536//D * (n1//D) has to be less than 65536.
This can often be determined by looking at the range of expected
values.
Example: This formula can be useful in data logging in a paged
memory array. The denominator D is the page size, which for the
AT45DB041 is 132 words per page, so the factor (65536//132) is 64,
precomputed. The formula allows quickly finding the offset of a byte
on the current page, given an absolute address, N. The largest value
of n1//132 is 131, and 131*64 is well under the 65536 constraint.
offset = 64 * (n1//D) + (n0//D)
Or, suppose the memory array is 496 pages of 132 words per page,
for a total of 65472 words. The next free position in the memory
array is determined by an offset wy inwords, plus an number of words
used, wx. The offset and the number used may either be large numbers,
so the sum wy+wx may at times generate a carry to double precision.
The memory is really a circular array modulo 65472. So the idea is to
find the remainder of the addition modulo 65472. That will be the
location of the next free word in the absolute memory address.
wz = wx + wy
carry = wz max wy - wy max 1 ' 1 if carry from previous add
address = wz//65472 + (carry * 64)
This is just an application of the above formula, with
65536//65472=64, a precomputed constant, and (n1//D) is simply the
carry, because n1 is either 0 or 1.
|
Theory. The double precision dividend is represented as
a polynomial in base b=2^16=65536. Let's just stick with a divisor of
100 for clarity: Formulae in red are the Stamp operators of integer
division and remainder, instead of floating point division.
z = (z1*65536 + z0)/100
The stamp has to divide and conquer. The division by 100 is
distributed across the terms.
z = (z1/100*65536) + (z0/100)
parse z1/100 as integer z1/100 and fraction z1//100/100:
= (z1/100*65536)+(z1//100/100*65536)+(z0/100)
The first term above is the high word of the quotient. The low
word needs more parsing by dividing 65536/100 into the integer part 655
and the fractional part 0.36:
q1 = (z1/100*65536)
q0 = (z1//100*65536/100)+(z0/100)
= (z1//100*(655+0.36))+(z0/100)
= (z1//100*655)+(z1//100*36/100)+(z0/100)+remainder
Note that the formula will never overflow. The first term is
655 times a number that will always be less than 100, so the product
will is always less than 99*655=64845. The second term can be as high
as 99*36/100=35. And the final term can be no greater than
65535/100=655. Adding up the three maximum values we get 64845+35+655 =
65535, which of course fits exactly in one 16-bit word. One subtle
issue, we must combine the two final terms:
= (z1//100*655)+(z1//100*36+z0/100)
Otherwise, the fractional remainder from the two separate
divisions by 100 can add up to more than one. Another way to write this
would be:
= (z1//100*655)+(z1//100*36/100)+(z0/100)
+(((z1//100*36//100)+(z0//100))/100)
where the final term combines the two fractional remainders
and divides those. That form is obviously more complicated than the one
just above.
Let's focus in on the remainder. The remainder has in general
a contribution both from the high word and from the low word. Again
think of the representation in base 65536:
z = (z1*65536 + z0)/100
We divided z1 by 100 to get an integer part, q1=z1/100 and a
remainder
z1//100/100*(65500+36)
^^^^^^^^--shown as a sum
^^^^^^^^^^^---this is a fraction <1
This remainder has to be added to the low word, and it
contributes both to the quotient and to the overall remainder from the
division. Concerning the contribuition to the overall remainder, which
be an operation modulo 100, we can drop the 65500, because it is
divisible by 100. This is a fundamental property of modular arithmetic.
See the section on basic arithmetic below for the distributive
properties of the // operator. The contribution from the high word to
the remainder is: z1//100 * 36//100. The contribution from the low word
is z0//100. Each of these terms may be a number from 0 to 99. The
overall remainder is the sum of these two terms, so the sum may be a
number as high as 198. We take the operation modulo 100 once again to
get the overall remainder:
rm = (z1//100*36//100)+(z0//100))//100
or, the same result, but slightly simpler formula
rm = (z1//100*36)+(z0//100))//100
-----
Special care is needed if the divisor is greater than 256.
Here is the modified formula for division by 1000:
q1=z1/1000
q0=z1//1000
rm=((q0**536*536//1000)+(q0*536//1000)+(z0//1000))
q0=(q0*65)+(q0**35127)+(z0/1000)+(rm/1000)
rm=rm//1000
The second term in the final expression for q0 is (q0**35127)
. In the original formul here, this would be (z1//1000)*536/1000. That
would blow up if the product z1//1000*536 is greater than 65536. In
Stamp math, the proportion 536/100 can be written as 35127/65536, which
is the effect of **35127. This will not blow up. We separately add in
the term z0/1000, and then the remainder term, rm/1000. The remainder
formally also involves the term (z1//1000)*536, but this multiplication
in general extends to double precision, and the upper word of that
product is z1//1000**536. The upper word is base 65536, so it
contributes to the overall remainder when divided by 1000. The *536
comes from this second multiplication by 65536 modulo 1000. The term
will not blow up, because its maximum value is 999**536=8 and
8*536=4288. For some divisors the product, (q0**B*B) will exceed 65535.
For example, the formula does not work for dv=10000, because the
maximum value of the term is then, 9999**5535=844, and
844*5535>65535. Many large divisors do not work. It just depends on
the remainder left when taking the chosen divisor into 65536. 5000 does
work.
|
|
Formula to kick out
decimal digits from a double precision number
|
top
|
The BASIC Stamp has no direct way to display double precision
numbers in decimal. For example, given the 32-bit number, $FAB40D35,
how do you display it in decimal? The Stamp can easily display that
in HEX using
debug ihex4 $FAB4, hex4 $0D35 ' displays $FAB40D35
but the Stamp's DEC modifier does not easily extend to double
precision. For example if you display the separate decimal parts, you
get the wrong answer.
debug dec5 $FAB4,dec5 $0D35 ' displays 6418003381
instead of the correct decimal value, which is 4,206,103,861. The
problem is the change of base, which is correctly calculated as
64180*216+3381.
The following program divides the double precision number by 100
several times in a row, until there is no remainder, to extract the
decimal digits and print them on the debug screen. Since the
remainders come off with the least significant digits first, the
program stores the digits in the SP ram of the BS2e, and when they
are all extracted it prints them out, most significant digits first.
The demo program generates random 32-bit double precision numbers,
displays them in hex using standard BS2 format, and then calls the
"showdubdec" subroutine to displays the same numbers in decimal. You
can use a numerical calculator to double check the results.
'{$STAMP BS2e}
wran var word ' for random numbers
wx var word ' most significant word
wy var word ' least significant
rm var byte ' remainder from division
ix var nib ' loop index
temp var byte ' temporary working variable
loop:
random wran ' make random number
wx=wran
random wran ' 2 words long
wy=wran
debug cr,hex4 wx,hex4 wy,tab ' show it in hex
gosub showdubdec100 ' convert and show it in decimal
pause 1000
goto loop ' do it again
showdubdec100:
for ix=4 to 0 ' 5 bytes can hold 10 digits
temp=wx//100 ' high remainder
wx=wx/100 ' high word of quotient
rm=((temp*36//100)+(wy//100)) ' remainder calc
wy=(temp*655)+(temp*36/100)+(wy/100)+(rm/100) 'low word of quotient
rm=rm//100 ' final remainder
put ix,rm ' store remainder
next ' ix next digits
' -- printout routine, digits stored in spRAM
for ix=0 to 4 ' print digits, most significant first
get ix,temp ' from spRAM
debug dec2 temp ' includes leading zeros
next
return
Here is a variation on the final printout routine, one that
supresses leading zeros. The variable rm here is used to keep track
of whether or not the first non-zero character has been printed, and
to branch to the appropriate printing command.
' -- printout routine, digits stored in spRAM
rm=0 ' nothing printed yet
for ix=0 to 4
get ix,temp
rm=temp max 1+(ix/4)+rm+rm ' 0 until 1st non-zero byte
' or until last byte
' >1 after first non-zero byte
branch rm,[showdub2,showdub1]
debug dec2 temp ' end up here to print leading zeros
goto showdub2
showdub1: ' branch here to print without leading zeros
debug dec temp
showdub2: ' branch here to print nothing
next
return
-----
And here is a variation that extracts the digits by a succession
of divisions by 10, instead of 100. The digits (up to 10 of them now)
stored as ascii codes in the scratchpad ram and then are printed out
in most significant first.
showdubdec10:
for ix=9 to 0 ' 10 bytes hold 10 digits, peal off 1s digit first
temp=wx//10 ' high remainder
wx=wx/10 ' high word of quotient
rm=((temp*6//10)+(wy//10)) ' remainder calc
wy=(temp*6553)+(temp*6/10)+(wy/10)+(rm/10) 'low word of quotient
rm=rm//10 ' final remainder
put ix,rm+48 ' store remainder converted to ascii
next ' ix next digits
' -- printout routine, digits stored in spRAM
for ix=0 to 9 ' print digits, most significant first
get ix,temp ' from spRAM (includes leading zeros)
debug temp ' print the ascii code, could be to LCD
next
return
|
Double precision
division, division by a variable (or a constant)
|
top
|
When a variable is in the denominator, instead of a
constant known at compile time, division is more problematic. The
formulae in the preceding section do not apply directly, because we
cannot precompute the factors that involve 65536. Our BASIC Stamp
counting goes only up to 65535.
Here are some ways to go about it. Another section on the
theory appears at the end of this article.
- Method 2 works when the divisor is less
than or equal to 257 and the dividend (numerator) is a double precision
number up to 32 bits. Some of the factors can be computed in advance if
the divisor is a constant. The method also works for other divisors if
the dividend (numerator) is restricted. For example, it works for all
divisors from 1 to 65535 if the numerator is restricted to 0 to 131071.
- Method 2 is most general and works for
cases where 0<divisor <32768 and 0<numerator <231.
This uses a loop structure for the main division.
Method 2: successive reduction. divisor up to
257, other divisors ad hoc.
This method works for all divisors up to and including 257 and
with all numerators up to 232. It also works on an ad-hoc
basis with other combinations of divisor and dividend, such as all
divisors<65536 when the dividend <131072. This method is my
favorite for most double precision division within its range of
applicability.
The actual division formula consists of the five lines of code
after the remark line labeled *division*. This provides both the
quotient and the remainder. The rest of the program is just the
overhead for the demo that generates random numbers to try out, and
then displays those numbers and the quotients and remainders for you
to check on your hex calculator.
' dubdiv2.bs2
' demo of double precision division, byte divisor
' (c) 2000 Tracy Allen, http://www.emesystems.com
' Given a double precision numerator up to 32 bits,
' and a divisor from 1 to 257,
' this routine calculates the quotient and the remainder.
' The demo picks numbers out of a hat and displays results
' on the debug screen in hex for verification.
' Other divisors are possible too, if the numerator is restricted.
' E.g., If the numerator is <131072 (2^17), then the divisor
' can be from 1 to 65535.
' do not allwo division by zero!
'
x var word ' random numbers for the demo
n1 var word ' most significant word of numerator
n0 var word ' least significant word of numerator
dv var byte ' divisor 1<=dv<=256
q1 var word ' most significant word of quotient
q0 var word ' least significant word of quotient
r0 var byte ' remainder 0<=r0<dv
k1 var word ' for check on accuracy of result, high word
k0 var word ' to compute quotient*divisor+remainder
' -arbitrary initialization--->
x=555
' -main loop----------->
loop:
pause 1000
random x ' pick a numerator
n0=x ' low word
random x
n1=x ' high word
random x ' pick a divisor
dv=x&$ff min 1 ' limit divisor to 8 bits and not zero
' ------------*division*------------------
r0=n1//dv ' remainder from high word
q1=65535//dv*r0//dv+r0+(n0//dv) ' temporary computation
q0=65535/dv*r0+(65535//dv*r0/dv)+(n0/dv)+(q1/dv) ' low word of quotient
r0=q1//dv ' final remainder
q1=n1/dv ' high word of quotient
'------*end of division*---------------
' -check by multiplying out------------
k1=q1*dv+(q0**dv) ' multiply quotient times divisor
k0=q0*dv+r0 ' and add remainder
k1=k0 max r0 - r0 max 1 + k1 ' carry from addition
debug cr,hex4 n1,hex4 n0,"/",hex2 dv,"= "
debug hex4 q1,hex4 q0," R=",hex2 r0 ' show result
debug " check=",hex4 k1,hex4 k0 ' should be the starting number
goto loop ' pick a new set of numbers...
The main constraint on the applicability of the method are the
quantities:
(65535/dv)*(n1//dv) and (65535//dv)*(n1//dv)
which must not overflow 16 bits. They will never overflow 16 bits
so long as dv<=257. The theory is outlined in a section below.
It will also work with other divisors and dividends provided
certain conditions are met.
For example, suppose you have 128kbyte memory for data logging,
you might need a quick way to calculate the maximum number of data
records it can accomodate, given the record length.
maxdat=131072/recordlength. The record length would not
usually exceed 257 bytes.
If the numerator is restricted to the range of 1 to 131071, then
the divisor can be any number in the range 0<dv<65535. Reason
as follows: The high word of the double precision numerator,
N<2^17, is either zero or 1. When n1=0 or 1, then n1//dv also
equals zero or one. So the two constraints shown above in red will
also always be less than 65536.
Here is the simplified division, when the numerator is restricted
to 17 bits. The code can be shortened in cases where you need only
the quotient q0 or only the remainder r0, or where the divisor dv
will always be greater than one.
' --*division, numerator <131072 (2^17)*-----
q1=65535//dv*n1//dv+n1+(n0//dv) ' temporary computation
q0=65535/dv*n1+(65535//dv*n1/dv)+(n0/dv)+(q1/dv) ' low word of quotient
r0=q1//dv ' final remainder (might be a word if dv>256)
q1=n1/dv ' high word of quotient
' ------*end of division*---------------
Here is another practical case. Often the divisor is a fixed
constant, known in advance at compile time. For example, you might
need a divide by 10 routine, to kick out the decimal digits of a
double precision number to a display. Terms like
65535//10=5 and
65535/10=6553 can be precomputed to save
a bit of code and execution time. This is very similar to the outcome
of method #1 above. The difference there is
that factors involving 65536 could be precalculated, whereas in the
current method, 65536 had to be treated as 65535+1. Method 1 is
simpler where the factor is a constant.
' ----*division by fixed constant, dv=10*------------------
r0=n1//10 ' remainder from high word
q1=5*r0//10+r0+(n0//10) ' temporary computation
q0=6553*r0+(5*r0/10)+(n0/10)+(q1/10) ' low word of quotient
r0=q1//10 ' final remainder
q1=n1/10 ' high word of quotient
' ------*end of division*---------------
Method
3: long division. divisor up to
32768.
The actual division formula consists of the eight lines of code
after the remark line labeled *division*. The rest of the program is
just the demo program, declaring variables, and converting between
standard binary and 16:15 representation. In early versions of this
algorithm, I had not calculated out the remainder. This version
computes both the quotient and the remainder.
' dubdiv3.bs2
' demo of double precision division, 15-bit divisor
' (c) 1999 Tracy Allen, http://www.emesystems.com
' Given a double precision numerator up to 31 bits,
' and a divisor up to 32768,
' this routine calculates the quotient.
' The demo picks dividends and divisors out of a hat
' and displays results on the debug screen
' in hex for verification.
'
n1 var word ' most significant word of numerator
n0 var word ' least significant word of numerator
dv var word ' divisor 1<=dv<=32768
x1 var word ' most significant word of quotient
x0 var word ' least significant word of quotient
z var word ' temporary variable for long division
' also remainder from division at end
rx var word ' for random number generator
ix var nib ' index for long division
'
' -arbitrary initialization--->
n1=555
n0=789
dv=22
' -main loop----------->
loop:
random rx ' pick a numerator
n1 =rx ' high word
n1.bit15=0 ' restrict it to 31 bits
random rx ' pick a numerator
n0=rx 'low word
random rx ' pick a divisor
dv = rx & $7fff ' & restrict it to 15 bits
debug cr,hex4 n1,hex4 n0,"/",hex4 dv,"= "
' ---*format conversion*---
n1=n1<<1+n0.bit15 ' convert numerator to 16:15 format
n0.bit15=0
' ----*division*----------------
x1=n1/dv ' high word
x0=0 ' initialize for long division
z=n1
for ix=14 to 0 ' long division, 15 bits
z=z//dv<<1
x0.bit0(ix)=z/dv
next
x0=x0+(n0/dv) ' result plus contribution from low word
' now find the remainder
z=(z//dv)+(n0//dv) ' combined remainder
x0=(z/dv)+x0 ' may have to add one to quotient
x1=x1+x0.bit15 ' add possible carry 16:15
x0.bit15=0 '
z=z//dv 'final remainder
' ----*end of division*----------
x0.bit15=x1.bit0 ' convert quotient to standard binary format
x1=x1>>1
' ---*end or format re conversion*---
debug hex4 x1,hex4 x0," remainder= ",hex4 z ' show result
pause 1000
goto loop ' pick a new set of numbers...
Theory for multiple precision division:
I include this section on theory for people who are interested in
such things, and also to remind myself how I got these results. It is
awfully easy to forget! This is all elementary math, but in a form
that is not taught much in schools.
THEORY 1: fundamentals of arithmetic
The primary thing to remember in division is how it relates to
multiplication. Consider the division of dividend N by divisor D. The
problem of division consists of finding the unique integer quotient and
integer remainder (0<=R<D) that satisfy
N = Q * D + R ' dividend = quotient*divisor + remainder
These integers can always be found. It is important to note
that the remainder is always less than the divisor. For example, the
problem 77/5 is viewed as 77 = 15*5+2, where 15 is the integer quotient
and 2 is the integer remainder. This can also be written with the
remainder as a fraction.
N/D = (Q*D + R)/D = Q + R/D ' where Q is the quotient and R is the remainder
77/5 = (15*5 + 2)/5 = 15 + 2/5 ' numerical example
In the first step, the number N is written as a quotient times
the divisor, plus the remainder. Then the division is distributed, so
we are left with an integer quotient and a proper fraction as a
fractional remainder.
In the PBASIC of the Stamp, ithe quotient is given by integer
division
Q=N/D
Because integer division on the Stamp discards the remainder.
Do not confuse the stamp's integer division with proper fractional
division. To emphasize which one I am talking about, I will put the
stamp math in red plain text, and the caluclator math with proper
fractions in italic black.
The integer remainder on the Stamp is given by the // operator,
R=N//D
In stamp language,
N = N/D * D + N//D
77 = 77/5 * 5 + 77//5
77 = 15 * 5 + 2
Keep in mind the following rules. Ordinary division
distributes over addition:
- (A+B)/C=(A/C)+(B/C)
And the associative and commutative rules of multiplication,
that terms can be grouped and done in any order.
(A*B)/C=(A/C)*B = A*(B/C)
Emphasize that this applies to ordinary division, but
decidedly not to integer division. For example, in ordinary division,
(5+7)/3 = 12/3 = 4 or 5/3 + 7/3 = 12/3 = 4.
But in integer division,
(5+7)/3 = 12/3 =4 but 5/3 + 7/3 = 1 + 2 = 3.
Similarly, in ordinary division,
5*7/3 = 35/3 = 11 2/3 or 5/3 * 7 = 11 2/3 or 5 * 7/3 = 11 2/3.
While in contrast in integer division,
(5*7)/3 = 35/3 = 11 or 5/3 * 7 = 1*7 = 7 or 5 * 7/3 = 5*2 = 10,
which gives three quite different answers. In the following we
will be careful to distinguish between places where we are using
ordinary division, and where we are referring to integer division as
the Stamp sees it. The ordinary kind of / will
be shown in larger, blacker type.
The modulus operator (//) is peculiar, and has the following
distributive rules. The modulus operator is strictly an integer
operation.
- Distributive over multiplication:
-
- (A*B)//C = ((A//C)*(B//C))//C
- or
- (A*B)//C = (A*(B//C))//C
- or
- (A*B)//C = ((A//C)*B)//C
These all need the final //c. For example,
(6*7)//4 = (42//2) = 2
or distributed...
(6//4)*(7//4)//4 = (2*3)//4 = 6//4 = 2
- Observe that it requires the final // oprator. The //
operator is also distributive over addition:
-
- (A+B)//C=((A//C)+(B//C))//C.
-
For example
(6+7)//4 = 13//4 = 1 or (6//4)+(7//4) = (2+3)//4 = 5//4 = 1
Again, the closing // is required.
Division is a matter of applying these rules over and over
again. Take a number that is too large for the stamp to handle, apply
the quotient:remainder formula, and rearrange the terms. Do it again if
necessary, until all the terms are within the range the stamp can
handle. Method 3 takes a different tack, long division, to resolve the
most problematic term.
|
THEORY 2: derivation of method #2
The problem is how to divide a double precision number N by a
single precision number D. The double precision number is written in
"base 65526" as:
N = N1*65536 + N0
Where the values of N1 and N0 are two separate words. The
division is:
N/D = (N1*65536 + N0)/D
and the result will be another number, which may in general
also be a double precision number.
N/D = Q1*65536 + Q0
and a remainder R0 ' 0<=R0<D
Here is the step by step derivation:
N/D = (N1*65536 + N0)/D
= (N1*65536/D) +(N0/D) ' distribute ordinary division
= (N1/D*65536 + (N0/D) ' associative, ordinary division
= ((Q1*D+R1)/D*65536 + (N0/D) ' arithemetic, Q1=N1/D, integer division, R1=N1//D
= (Q1 + R1/D )*65536 + (N0/D) ' distributive, cancel D
=(Q1*65536) + R1/D*65536 + N0/D ' distributive, Q1 is high word of quotient
' and R1/D is a proper fraction
That resolves the high word of the quotient, simply (Q1*65536).
On the stamp, the high word is simply Q1=N1/D,
the result of integer division. Now let's move on to the low word of
the quotient, which has contributions from the remaider of the division
of the high word, and from the division of the low word. R1=N1//D is the remainder from the high word.
R1*(65536/D) + N0/D
= (R1*(65535 + 1)/D) + N0/D ' trick, split 65536=65535+1
= (R1*(65535/D + 1/D) + N0/D ' distribute ordinary division by D over addtion
= R1*((Q2*D+R2)/D + 1/D) + N0/D ' arithmetic, Q2=65535/D, R2=65535//D.
= R1*(Q2 + R2/D + 1/D) + N0/D ' distribute ordinary division by D over addition
= (R1*Q2) + (R1*R2/D) + (R1/D) + N0/D ' distribute multiplication by R1 over addition
= (R1*Q2) + ((Q3*D+R3)/D) + (R1/D) + N0/D ' arithmetic, Q3=R1*R2/D, R3=R1*R2//D
= (R1*Q2) + Q3+ (R3/D) + (R1/D) + N0/D ' distribute ordinary division by D over addition
= (R1*Q2) + Q3+ (R3/D) + (R1/D) + (Q4*D+R4)/D ' arithmetic, Q4=N0/D, R4=N0//d
= (R1*Q2) + Q3+ (R3/D) + (R1/D) + Q4 + R4/D ' distribute ordinary division by D over addition
= (R1*Q2) + Q3+ + Q4 (R3/D) + (R1/D) + R4/D ' collect remainders
= (R1*Q2) + Q3+ + Q4 + (R3 + R1 + R4)/D ' distribute ordinary division over addition
= (R1*Q2) + Q3+ + Q4 + (Q5*D+R5)/D ' arithmetic Q5=(R3+R1+R4)/D, R5=(R3+R1+R4)//D
= (R1*Q2) + Q3+ + Q4 + Q5 + R5/D ' distribute ordinary division by D over addition
This is the desired result. All the
terms are now integer division or modulus operations as done on the
stamp, and there are no remainders greater than one. Each term in the
sum will be less than 65535, so long as D is less than or equal to 257.
quotient high word = Q1 = N1/D
quotient low word Q0 = (R1*Q2) + Q3+ + Q4 + Q5
= (N1//D)*(65535/D)+((N1//D)*(65535//D)/D)+N0/D+(((N1//D)*(65535//D)+(N1//D)+(N0//d))/D)
remainder = R5 = (R3+R1+R4)//D
= ((N1//D)*(65535//D)+(N1//D)+(N0//d))//D
The program for method 2 saves some repetition of code by
first calculating the terms (N1//D) and
((N1//D)*(65535//D)+(N1//D)+(N0//d)). It also has some minor changes in
notation.
The individual remainders that make up the Q5 and R5 term are
all individually less than one, but their sum can be greater than one
and contribute to the overall integer quotient when divided by D. The
overall remainder is what is left after that final division.
What remains is to analyze the
limitations of the method, to see what combinations of values will lead
to integer overflows. Going term by term, one can see that each term
will always stay within the bounds of one 16 bit word so long as the
the divisor is less than or equal to 257. Other cases may be addressed
on an ad hoc basis. For example, if N1 can be no greater than
one, then the divisor can take on any value in the range 1 to 65535.
|
THEORY 3: derivation of method 3
format conversion
In methods 1 and 3, the double precision number will be
allowed to have up to 31 bits. That is so that it can be represented in
16:15 form. I need the most significant bit of the lower word as a
carry/borrow. Method 2 does not require format conversion.
Here is a binary number in 15:16 form, as two groups of 16
bits, words on the BASIC Stamp:
{0nnnnnnnnnnnnnnnn} {nnnnnnnnnnnnnnnn}
^^^^^^^^^^^^^^^^--16 significant bits in low word
^^^^^^^^^^^^^^^^^--15 siginficant bits in high word, 16th bit =0
To transform to 16:15 form:
most sig. bit from low word shifts up to high word
;<--;
{nnnnnnnnnnnnnnnnn} {0nnnnnnnnnnnnnnn}
^^^^^^^^^^^^^^^^--15 significant bits in low word, 16th bit=0
^^^^^^^^^^^^^^^^^--16 siginficant bits in high word
To transform back to 15:16 form:
least sig. bit from high word shifts down to low word
;->;
{0nnnnnnnnnnnnnnnn} {nnnnnnnnnnnnnnnn}
^^^^^^^^^^^^^^^^--16 significant bits in low word
^^^^^^^^^^^^^^^^^--15 siginficant bits in high word, 16th bit =0
And here are the transforms as implemented on the Stamp.
N0 var word ' least significant word
N1 var word ' most significant word
N1=N1<<1+N0.bit15 : N0.bit15=0 ' convert 15:16 to 16:15
N0.bit15=N1.bit0 : N1=N1>>1 ' convert 16:15 to 15:16
A double precision number, DPN is represented in the stamp as
follows, which depends on the notation
DPN = N1*65536 + N0 ' numerator in 15:16 notation
DPN' = N1'* 32768 + N0' ' numerator in 16:15 notation
Italic indicates that the formula is "in theory", not a
calculation to be carried out by the stamp.
It is important to understand that this is a positional
notation in either base 32768 or in base 65536, and the transform is a
simple change from one base to the other. Think about what happens when
N0=32767. When you add one to that, the number is 32768. In 15:16
notation, this value is still held within on 16 bit word. The high bit
of that word, N0, is set. In 16:15 notation, adding 1 to 32676
generates a carry. The value of N1 becomes 1, while the value of N0
returns to zero. The 1 in N1 represents 1 times 32768.
derivation
Division of the two-word dividend (numerator) by a divisor,
Dv, results in an integer quotient and an integer remainder.
DPQ = DPN/Dv = (N1*32768 + N0) / Dv ' quotient
DPR = DPN//Dv = (N1*32768 + N0) // Dv ' remainder 0<=DPR<Dv
As on the Stamp the "/" and the "//" will denote integer
division and the remainder after the division, respectively. The
problem on the Stamp is that we can't just do things in that order,
because every step of the calculation on the stamp has to stay within
the bounds of one 16 bit word. We have to be tricky and do things in
the right order--divide and conquer.
First think about the overall remainder from the division:
DPR = (N1*32768 + N0) // Dv
This will be a number in the set (0,1,...,Dv-1). The problem
is, we can't just multiply N1*32768 and add N0, because that will
overflow the 2^16 workspace. That would happen for every N1>1!
and in effect insert an additional //65536 term that whacks
the result. In general the expression, A // C = A // B // C is not
true.
The modulus operator (//) has the following distributive
properties:
- Distributive over multiplication:
- (A*B)//C = ((A//C)*(B//C))//C
- Distributive over addition:
- (A+B)//C=((A//C)+(B//C))//C.
(To prove these properties, write A=a1*C+a0, and B=b1*C+b0 and
carry out the multiplication. Terms with a C drop out. See any text on
linear algebra.)
Using these facts, the remainder can be kept within bounds of
one word. On the Stamp, let's first assume that the divisor is less
than or equal to 256. Then the following Stamp formula will give the
remainder,
Xr = N1//Dv*(32768//Dv)+(N0//Dv))//Dv ' remainder
'^^^^^^ ^^^^^^^^^ ' 0 <= Xr < 256
' A B
The terms A and B are each less than 256, so their product is
less than 65536. That is, so long as Dv<=256. In method 1 above, we
used this formula to calculate the remainder, even before computing the
division itself. In method 3 above, when the divisor could be larger,
we had to wait and compute the integer division first and then the
remainder.
Now on to the division proper. We can distribute the division
over the terms:
DPN = (N1*32768 + N0) / Dv
= (N1*32768)/Dv + N0/Dv + (N1*32768//Dv + N0//Dv)/Dv)
^^^^^^^^^^^^^^^^^^^^^
each remainder < DV, but sum may be >Dv
this term is either 0 or 1.
And further distributing the first term:
quotient remainder
------------- ----------------
= (N1/Dv*32768) + (N1//Dv)*32768/Dv + N0/Dv + (N1*32768//Dv + N0//Dv)/Dv)
^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
high word this whole term is <32768 and is the low word
Now focus on the term, (N1//Dv)*32768/Dv. One way to
group this is:
(N1//Dv)*32768/Dv = [(N1//Dv)/Dv] * 32768
The term in square brackets is between zero and (Dv-1)/Dv . We
can calculate it using the binary long division algorithm to 15 bits.
The binary
long division algorithm divides N1//Dv by Dv and at the same time
automatically multiplies times 32768. This is the approach in method 3
above.
|
Here is a link to
divison of numbers
having an arbitrary size and a note on the interpretation of fixed
point fractions.
<top> <index>
<home>
 < mailto:info@emesystems.com
>
< mailto:info@emesystems.com
>